For a few months now, we’ve been talking about framing and how it affects users’ perceptions. In December, I talked about how the framing of something as simple as a return or exchange policy can make it appear that one exists, one doesn’t exist, or both exist under weird descriptions. Last month, I showed how changing the domain of the problem can help with problem solving—-specifically that putting a problem in the common domain can make the problem solvable. (I will admit, though, that some people still have difficulty seeing that the two problems presented last month were actually identical.)
One of the issues often encountered in interface design is having an interface that represents a problem in a way that, while it may be accurate or even understood by some, it is not in a format that is easily perceived and processed by the average user. As interface designers, we often see that the underlying architecture of the system is protruding through to the user interface. Only if you have a background in computer science, or were responsible for developing the underlying architecture, can such an interface even make sense.
It’s hard to find a clear example for this particular issue, so I’ve chosen to play a game with you instead that demonstrates that how a task is presented can have a significant impact on your ability to perform the task. Since, as the designer, we can decide how to present the task, we can make the game as hard or as easy as we would like. So let’s play the Game of 15.
In the Game of 15, all numbers between one and nine are in the game to start with. (We will not use the number zero and we will not be using multiple-digit numbers.) Each player (you and I will be playing each other) will alternate picking numbers. Once a player has taken the number, it belongs to that player.
The object of the game is to try to collect numbers until you have any three numbers that add up to 15. For example, you would win if you collected a 2, a 5, and an 8, since these three numbers add up to 15. Similarly, you would win if you have a 1, a 5, and a 9, since they also add up to 15. In fact, there are eight possible combinations of three numbers (using numbers 1 through 9 only once) that add up to 15.
As long as you have any three numbers equaling 15, you win. But remember, you’re playing against an opponent (me, in this case). You have to be careful in making your selection of numbers. While you are trying to collect three numbers for yourself that will add up to 15, so am I. That means you may need to take a number before I do to keep me from getting a set of numbers that add up to 15 first. And I may do the same to keep you from winning.
Ready to play? I’ll get us into a game. I’ll start first (because I’m writing this).
- I take the 4.
- You take the 2.
- Then I take the 8.
- You don’t want me to get to 15 in my first three moves, so you take the 3.
- Then I take the 5.
What number should you take next? By the way, there is only one correct answer if you don’t want me to win in my next move. Do you know what number that is?
If this game is too hard, we might want to play something a bit easier. Let’s play tic-tac-toe. I assume I don’t have to tell you the rules. In fact, I’m going to show you a game in progress and ask you to tell me what your next move should be. I’ll be X’s and you be O’s. Given the game below, what move should you make?
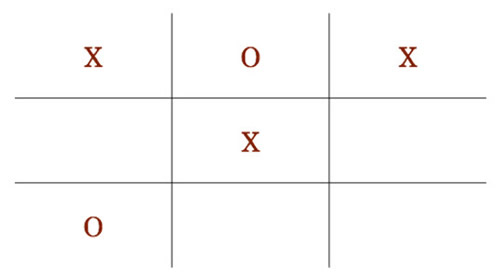
If you said the lower right square, you’re correct. You need to block me from winning in my next move.
OK, if you haven’t figured out where I’m going yet, we’re playing the Game of 15 in a different way. This time, all the numbers from 1 through 9 are placed in an array with the numbers arranged so that three numbers in any direction will add up to 15. The numbers I picked are crossed out. The numbers you picked are circled.
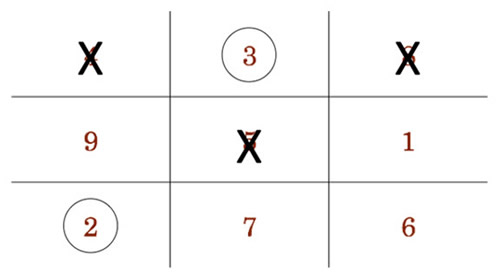
Do you see now the number you would need to pick in your next turn?
Just presenting a problem to users is not enough. Just presenting information and hoping users will understand it is not enough. A clever designer needs to figure out how best to present any information or problem so that users can fully understand it.



