In December I talked a bit about framing. There are several types of framing, including temporal framing, outcome framing, and goal framing. How we frame something does not change the essence of that thing. However, the framing we apply can have a profound effect on how we perceive a problem, on our decision making, and on our ability to solve a problem. Here’s an example.
In the figure below is a set of cards that have a number on one side and the name of a color on the other side. The person who created the cards was given a rule to follow. The rule was: “If a card has an even number on its face, it must have a primary color on its opposite face.”
Here’s the problem to solve. Given the four cards in the figure below, how many cards do you have to turn over to see if this rule was followed?
Most people have difficulty determining the correct answer to this problem. Many say you need to test all four cards. This is incorrect. The truth is you only need to test two of them. Do you know which two? And do you know why only those two? If not, let’s try a different problem.
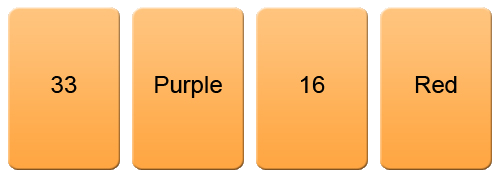
In the figure below is another set of four cards that have an age on one side and a type of drink on the other side. The person creating these cards was given a rule to follow as well. The rule was: “Alcohol can only be on a card if the age on the card is greater than 21.”
Given the four cards in the figure below, how many cards do you have to turn over to see that this rule was followed?

The answer is two cards—-the second and third. Did you get it right? And can you explain why just these two cards?
First, the rule does not suggest any restriction to an age over 21 so there is no need to check the first card. It represents an age of 33. The back of this card could have an alcoholic drink or a have a non-alcoholic drink and still follow the rule. Similarly, there is no restriction on the age associated with non-alcoholic drinks, so the last card does not need to be checked. The non-alcoholic drink of Sprite can be associated with an age higher than or less than 21. Almost everyone gets this problem correct and can explain why.
If you look back at the first set of cards, you’ll notice these two problems are identical and have identical solutions. You only need to test the second and third cards in both sets. There is no rule about what kind of color is supposed to be on the back of a card with an odd number on the front (the first card); nor is there a rule about whether or a card with a primary color on it (“Red”) should have an odd or even number on the back of it.
The second version of the problem takes the same information and places the problem in a frame of reference that we have experience with. The theoretical problem becomes a concrete one. The abstract problem becomes familiar and clear. Next month, we’ll learn the game of 15s and see another example of how, as designers, we can make problem solving hard or easy for users through framing.



